위 이미지를 클릭하시면 인터넷으로 바로 문제를 풀어 보실수 있습니다.
(해설, 모의고사, 오답노트, 워드, 컴활, 정보처리 상설검정 프로그램 기능 포함)
전자문제집 CBT란?
종이 문제집이 아닌 인터넷으로 문제를 풀고 자동으로 채점하며 모의고사, 오답 노트, 해설까지 제공하는
무료 기출문제 학습 프로그램으로 실제 상설검정에서 사용하는 OMR 형식의 CBT를 제공합니다.
최신 9급 국가직 공무원 수학 필기 기출문제(해설) : [다운로드]
9급 국가직 공무원 수학 필기 기출문제(해설) 및 전자문제집 CBT 2021년04월17일| 1. | 등식 (2+i)x+(1-i)y= 1+2i 를 만족시키는 실수 x, y에 대하여 (x+yi)4의 값은? (단, i = √-1) |
정답 : [1]☜ 블럭 설정하면 보임
정답률 : 29%
| | <문제 해설>
2x + y = 1
+) x - y = 2
----------------
3x = 3
x=1, y=-1
(1-i)^2 = 1-2i-1 = -2i
(-2i)^2 = -4
[해설작성자 : 한 때 수학 잘 했던 사람] |
|
| 2. | x2 + x – 1 = 0일 때, x3 + 3x2 + x + 2의 값은? |
정답 : [2]☜ 블럭 설정하면 보임
정답률 : 38%
| | <문제 해설>
x^3 + 3x^2 + x + 2 = (x^2 + x - 1)(x + 2) + 4
주어진 문제에 보면 x^2 + x - 1 = 0 이기 때문에
0(x + 2) + 4 = 4
[해설작성자 : 한 때 수학 잘 했던 사람] |
|
| 3. | 실수 x에 대한 두 조건 p : x2 - x – 6 ≤ 0, q : x < a에 대하여 p가 q이기 위한 충분조건이 되도록 하는 정수 a의 최솟값은? |
정답 : [4]☜ 블럭 설정하면 보임
정답률 : 24%
| | <문제 해설>
p: x^2 - x - 6 = (x-3)(x+2) <= 0, -2 <= x <= 3
q: x < a
q는 충분조건이므로 p를 모두 포함 해야 한다. 그러니 a는 4보다 커야 한다. 그러므로 최솟값은 4
[해설작성자 : 한 때 수학 잘 했던 사람] |
|
| 4. | 함수 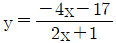 의 그래프가 지나지 않는 사분면은? 의 그래프가 지나지 않는 사분면은? |
정답 : [1]☜ 블럭 설정하면 보임
정답률 : 26%
| | <문제 해설>
2 | 1
ㅡ + ㅡ
3 | 4
분수에서 분모는 0이 되면 안되기 때문에 2x+1=/=0 이다. x는 -1/2이 될 수 없다.
y는 x를 무한대로 보낼 경우가 될 수없다. ---> 쉽게 말하면 -4x/2x =/=y 이다. y는 -2가 될 수 없다.
x = -1/2, y = -2 선을 지나지 않는다.
y = ax + b 에서 a가 음수이기 때문에
」|
ㅡ+ㅡ
「|-
이런 식으로 지난다.( 직접 그리는게 쉬운데...)
그러므로 제1사분면을 지나지 않는다.
[해설작성자 : 한 때 수학 잘 했던 사람] |
|
| 5. | x에 대한 이차방정식 x2 - 2kx – k2 = 0의 두 실근을 α, β라 하자. 1 ≤ k ≤ 4에서 (α+2)(β+2)의 최댓값을 M, 최솟값을 m이라 할 때, M-m의 값은? |
정답 : [4]☜ 블럭 설정하면 보임
정답률 : 23%
| | <문제 해설>
x^2-2kx-k^2=(x-alpha)(x-beta) 이고, x=-2를 대입하면, 4+4k-k^2=(2+alpha)(2+beta)입니다.
따라서 -k^2+4k+4 = -(k-2)^2+8 이므로 1<=k<=4에서 최댓값은 8, 최솟값은 4입니다.
따라서 M-m=4
[해설작성자 : 지식보부상] |
|
| 6. | -2 ≤ x ≤ 2에서 함수 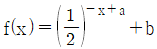 의 최댓값이 7, 최솟값이 41/8 일 때, 상수 a, b에 대하여 a+b의 값은? 의 최댓값이 7, 최솟값이 41/8 일 때, 상수 a, b에 대하여 a+b의 값은? |
정답 : [3]☜ 블럭 설정하면 보임
정답률 : 18%
| | <문제 해설>
(1/2)^(-x+a)+b = 2^(x-a)+b 이므로
2^x 꼴의 함수이므로 x=2에서 최대, x=-2에서 최솟값을 갖는다.
2^(2-a)+b = 7
2^(-2-a)+b = 41/8
연립방정식으로 풀어도 되지만 두번째 식에서 1/8이 나오는걸 보아 => a = 1
마찬가지로 두번째 식에서 2^(-3)+b = 41/8 = 5+1/8 => b = 5
=> a+b = 6
[해설작성자 : 찍먹] |
|
| 7. | 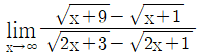 의 값은? 의 값은? |
정답 : [2]☜ 블럭 설정하면 보임
정답률 : 26%
|
| 8. | 두 사건 A, B에 대하여 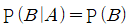 이고, P(A) - P(B) = 1/6, P(A∩B) = 1/6일 때, P(B)의 값은? 이고, P(A) - P(B) = 1/6, P(A∩B) = 1/6일 때, P(B)의 값은? |
정답 : [2]☜ 블럭 설정하면 보임
정답률 : 11%
| | <문제 해설>
우선, P(B|A) = P(A and B) / P(A) 이다. (A를 전체로 봤을 때의 B의 비율)
조건에 의해 P(A and B) / P(A) = P(B|A) = P(B) 이므로,
P(A)P(B) = P(A and B) 이다.
즉, P(A)P(B) = 1/6
두 연립방정식을 풀면된다.
P(A)-P(B) =1/6
P(A)P(B) = 1/6
그런데 두 수를 곱해서 1/6이 나올려면 1/2, 1/3이 적절하다. (보기와 2번 방정식으로부터 유추)
P(B) = 1/3
[해설작성자 : 찍먹] |
|
| 9. | 두 함수 y = x2 - 12(x≥0)와 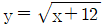 의 그래프는 한 점 (a, b)에서 만난다. a+b의 값은? 의 그래프는 한 점 (a, b)에서 만난다. a+b의 값은? |
정답 : [1]☜ 블럭 설정하면 보임
정답률 : 26%
| | <문제 해설>
정석은 x^2 - 12 = y = root(x + 12) 로 부터 양변을 제곱하여 4차 방정식을 풀면된다.
=> (x^2 - 12)^2 = x + 12
=> x^4 - 24x^2 + 144 = x + 12
=> x^4 - 24x^2 - x + 132 = 0
=> (x-4)(4x^3 + 4x^2 - 8x - 33)
...
그런데, 두 함수 모두 (a,b)를 지나는데, a+b의 값이 8,10,12,14 중 하나이므로 root 값을 갖지 않는다.
즉, (a,b)를 지날때, b = root(a+12) 값이 정수이다.
제곱수 16을 만들기 위해 x 에 4를 넣으면, (x>=0 제곱수 1,4,9 는 x<0 일 때에 속함)
4^2-12 = 4 = root(4+12) (=4)
=> (a,b) = (4,4)
=> a + b = 8
[해설작성자 : 찍먹] |
|
| 10. | 첫째항이 1/3, 공비가 r(r≠0)인 등비수열 {an}의 첫째항부터 n제항까지의 합을 Sn이라 할 때, S4 - S2 = a22이다. S4 = q/p일 때, q의 값은? (단, p, q는 서로소인 자연수) |
정답 : [1]☜ 블럭 설정하면 보임
정답률 : 16%
| | <문제 해설>
a_1 = 1/3
a_2 = 1/3 * r
a_3 = 1/3 * r^2
a_4 = 1/3 * r^3
S_1 = a_1
S_2 = a_1 + a_2
S_3 = a_1 + a_2 + a_3
S_4 = a_1 + a_2 + a_3 + a_4
이므로,
S_1 = 1/3
S_2 = 1/3 * (1 + r)
S_3 = 1/3 * (1 + r + r^2)
S_4 = 1/3 * (1 + r + r^2 + r^3)
=> S_4 - S_2 = 1/3 * (1 + r + r^2 + r^3) - 1/3 * (1 + r) , (a_2)^2 = (1/3 * r)^2 = 1/9 * r^2
= 1/3 * (r^2 + r^3)
이므로,
1/3 * (r^2 + r^3) = 1/9 * r^2
=> 3 * (r^2 + r^3) = r^2
=> 3r^3 + 2r^2 = 0
=> r^2(3r + 2) = 0
이때, r이 0이 아니므로, r = -2/3
그러므로,
S_4 = S_2 + (a_2)^2
= (1/3 * (1 + r)) + (1/9 * r^2)
= (1/3 * 1/3) + (1/9 * 4/9)
= 1/9 + 4/81
= 13/81
그러므로,
13/81 = q/p
=> q = 13
[해설작성자 : 찍먹] |
|
| 11. | 빨간 공 3개, 파란 공 4개가 들어 있는 주머니에서 임의로 2개의 공을 동시에 꺼낼 때, 꺼낸 공의 색이 다를 확률은? |
정답 : [3]☜ 블럭 설정하면 보임
정답률 : 32%
| | <문제 해설>
(4/7*3/6)+(3/7*4/6)=4/7
[해설작성자 : 쭈니] |
|
| 12. | 함수 y = 3cosbx + c의 그래프가 다음 그림과 같을 때, 상수 b, c에 대하여 b+c의 값은? (단, b>0) |
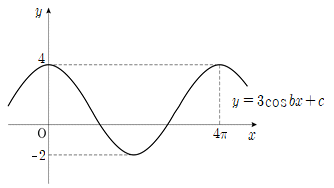
정답 : [2]☜ 블럭 설정하면 보임
정답률 : 22%
|
| 13. | 부등식 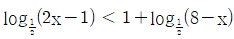 를 만족시키는 모든 정수 x의 개수는? 를 만족시키는 모든 정수 x의 개수는? |
정답 : [3]☜ 블럭 설정하면 보임
정답률 : 21%
|
| 14. | 함수 f(x)= x3- 2x2+ 4x- 1에 대하여 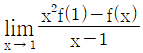 의 값은? 의 값은? |
정답 : [1]☜ 블럭 설정하면 보임
정답률 : 23%
|
| 15. | 원 C1 : x2+y2+4x-8y-5=0을 직선 y=x 에 대하여 대칭이동한 원을 C2라 할 때, 두 원 C1, C2의 중심 사이의 거리는? |
정답 : [4]☜ 블럭 설정하면 보임
정답률 : 23%
| | <문제 해설>
C1의 중심좌표 (-2,4)를 y=x에 대하여 대칭이동을 할 경우, C2 (2.-4)
두 점 사이의 거리 = 4*(5)^(1/2)
[해설작성자 : 민초돼지] |
|
| 16. | 두 확률변수 X와 Y는 각각 정규분포 N(10, 32)과 N(m, 22) 을 따른다. 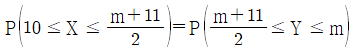 일 때, 상수 m의 값은? (단, m > 11) 일 때, 상수 m의 값은? (단, m > 11) |
정답 : [2]☜ 블럭 설정하면 보임
정답률 : 20%
|
| 17. | 함수 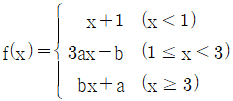 가 모든 실수 x에서 연속일 때, 가 모든 실수 x에서 연속일 때, 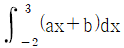 의 값은? (단, a, b는 상수) 의 값은? (단, a, b는 상수) |
정답 : [3]☜ 블럭 설정하면 보임
정답률 : 24%
|
| 18. | 원 x2+6x+y2-8y+20=0과 직선 2x+y+a=0이 만나도록 하는 실수 a의 최댓값은? |
정답 : [4]☜ 블럭 설정하면 보임
정답률 : 16%
|
| 19. | 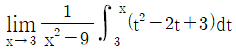 의 값은? 의 값은? |
정답 : [3]☜ 블럭 설정하면 보임
정답률 : 26%
| | <문제 해설>
f(t)=t^2-2+3 , F(t)= ∫t^2-2+3 이라고 합시다
식을 변형하면
lim = F(x)-F(3)/(x+3)(x-3)=f(3)/6이 됩니다.
그러므로 9-6+3/6 = 1
[해설작성자 : 규] |
|
| 20. | 사차함수 f(x)와 삼차함수 g(x)에 대하여 h(x) = f(x) - g(x)라 하자. y = f′(x)와 y = g′(x)의 그래프가 다음 그림과 같을 때, 함수 h(x)가 극대가 되는 x의 값은? |
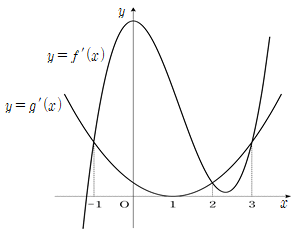
정답 : [3]☜ 블럭 설정하면 보임
정답률 : 13%
|
9급 국가직 공무원 수학 필기 기출문제(해설) 및 CBT 2021년04월17일을 이용해 주셔서 감사합니다.
, 필기, 기출문제, 전자문제집, CBT, 온라인, 모의테스트, 모의고사

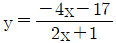 의 그래프가 지나지 않는 사분면은?
의 그래프가 지나지 않는 사분면은?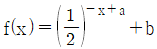 의 최댓값이 7, 최솟값이 41/8 일 때, 상수 a, b에 대하여 a+b의 값은?
의 최댓값이 7, 최솟값이 41/8 일 때, 상수 a, b에 대하여 a+b의 값은?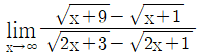 의 값은?
의 값은?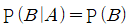 이고, P(A) - P(B) = 1/6, P(A∩B) = 1/6일 때, P(B)의 값은?
이고, P(A) - P(B) = 1/6, P(A∩B) = 1/6일 때, P(B)의 값은?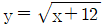 의 그래프는 한 점 (a, b)에서 만난다. a+b의 값은?
의 그래프는 한 점 (a, b)에서 만난다. a+b의 값은?
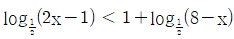 를 만족시키는 모든 정수 x의 개수는?
를 만족시키는 모든 정수 x의 개수는?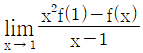 의 값은?
의 값은?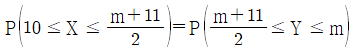 일 때, 상수 m의 값은? (단, m > 11)
일 때, 상수 m의 값은? (단, m > 11)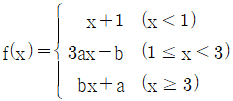 가 모든 실수 x에서 연속일 때,
가 모든 실수 x에서 연속일 때, 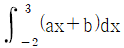 의 값은? (단, a, b는 상수)
의 값은? (단, a, b는 상수)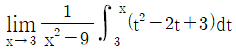 의 값은?
의 값은?